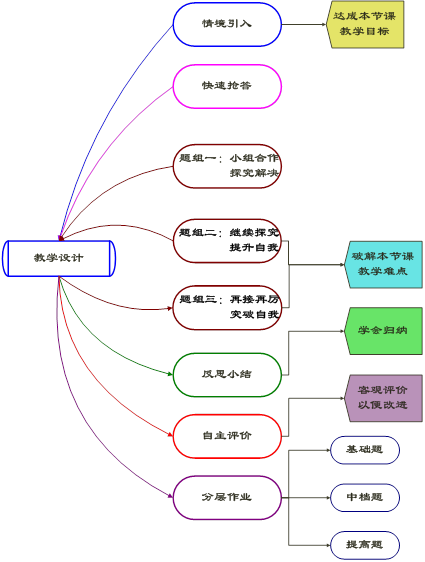
回顾本节课的教学过程：

课堂开端由一道简单的引例入题，提出问题：1.点在反比例图象上移动时，矩形的面积是否变化？2.改变K的值矩形的面积又怎样变化？即时触动学生的思维，进而回忆旧知：反比例函数有关的知识，切入问题自然，目的明确。

继而在师生的双边活动中学生通过类比方法轻易解决抢答题，此时几乎让所有学生都获得成功感，课堂气氛自然活跃起来。

在学生意犹未尽的情况下，立即让学生初试题组一，过程紧凑不失时机，全程以反比例函数与图形面积问题为中心，由易到难，由浅入深，层层递进，不断激荡学生的学习思维.由学生自己讲评题，充分调动学生的学习积极性，不断增强学生的自信心。

题组二是根据已知条件及图像信息，运用转化思想解决问题，在不断总结方法的同时获得更丰富的解题思想，让学生达到变“要我学”为“我要学”。

最后设置了题组三的提高题及课后作业，关注到学生的差异，让优生“吃得饱”学困生“有得吃”，充分体现隐性分层教学的思想。

课上完了，意未尽，本课成功在于：

1.利用网上资源进行选材，把学生零散的知识归类进行系统再分析，归纳解题方法，为学以致用提供指路明灯；

2.题型设计中渗透了反比例函数与直角三角形、矩形、四边形等图形面积，由易到难，充分关注到学生的个性差异，学生感兴趣思考解决，从而达成本节教学目标；

3.注重了数学思想方法的渗透，在每个例题的呈现中鼓励学生从题目已知出发结合图形进行分析，学会数与形的转化，从而突破难点，同时不失时机总结出其数学思想的方法：转化的思想、数形结合法，真正培养了学生的解题习惯。

不足在于：

1.本课设计还须在题目中多下功夫，认真读出题目的内涵，深挖其价值，以求触动每个学生的思维，使其有所获；

2.本节课的设计，虽然借助网上有用资源加以整合来可化难为易，但学生在题海中徘徊的时间较多，还未达到系统整理知识的目的；

3.为了拓宽视野（三组题），削减了学生的思考、讨论时间，以致有的学生反应较慢，未能跟上进度，影响课堂效率。

（初中数学组马娜）